
Mündəricat:
- Müəllif John Day day@howwhatproduce.com.
- Public 2024-01-30 07:43.
- Son dəyişdirildi 2025-01-23 12:54.


Ayın sonunda aylıq töhfə ilə mürəkkəb faizlərin hesablanması proqramı.
TheCalculatorSite.com saytından götürülmüş düstur: Əsas faiz üçün mürəkkəb faiz: P (1 + r/n)^(nt) Seriyanın gələcək dəyəri: PMT × (((1 + r/n)^nt - 1)/(r/ n))
Addım 1: İstifadəçidən məlumat alın

İstifadəçidən tələb olunan məlumatları daxil etməsini xahiş edin:
prinsipalinput = giriş ("Əsas məbləği daxil edin:") illik nisbət = giriş ("İllik dərəcəni daxil edin:") numberoftimescompoundedinput = giriş ("Faizin ildə neçə dəfə birləşdirildiyini sayını daxil edin:") yearsinput = giriş ("İllərlə vaxt:") monthcontributioninput = input ("Aylıq töhfə məbləğini daxil edin:")
Addım 2: Məlumatları çevirin

Məlumat tam ədədlərə çevrilməli olan bir sətir olaraq daxil edilir# Daxil edilən girişləri sətirlərə çevir (aylıq töhfə)
Addım 3: Birləşdirilmiş Faiz və Üstünlük Hesablayın

Birincisi, mürəkkəb faizi üstəgəl hesablayın: # mürəkkəb faizi əsas prinsiplə hesablayın əvvəlcədən sayı = (1 + (illik nisbət/ədədlərkompounded)) # çap ("İlkin nömrə:", ilkin ədəd) qaldırılmış güc = (sayı bir neçə dəfə * il) # çap ("Yüksəldildi gücə: ", yüksəldilmiş güc) mürəkkəbinterestplusprincipal = əsas*(ilkin sayı ** yüksəlmiş güc) çap (" Mürəkkəb faiz üstəgəl əsasdır: ", mürəkkəb maraqlararası)
Addım 4: Gələcəyin Dəyərini Hesablayın

Sonra əmanətlərlə gələcək dəyəri hesablayın# İndi dövrün sonunda qoyulan əmanətlərlə gələcək dəyərinizi hesablayın# Düsturdan istifadə edərək: Aylıq Ödəniş × (((((1 + r / n)^(nt)) - 1) / (r /n)) # r = illik faiz dərəcəsi # n = dövr başına birləşmələrin sayı (adətən aylarla) # t = pulun qoyulduğu vaxt (adətən illərlə)
oneplus = (1+ (illik rütbe/sayılar) birləşdi)) yüksəldilmiş güc2 = ((sayılar dəfə birləşən*illər)) qiymətləndirilmiş sayımlar = illik nisbət/sayılar zamanlar birleşmiş halfdone = ((depozitlərlə: , depozitlərlə gələcək dəyər) totalamount = mürəkkəbinterestplusprincipal + depozitlərlə gələcək dəyər
Addım 5: Kod
# Ayın sonunda aylıq töhfə ilə mürəkkəb faizi hesablamaq proqramı
# Əvvəlcə düsturdan istifadə edərək əsas faiz üçün mürəkkəb faizi hesablayın: A = P (1 + r/n) ** (nt) # r = illik faiz dərəcəsi # n = dövr başına birləşmələrin sayı (adətən aylarla) # t = vaxt prinsipialput = giriş ("Əsas məbləği daxil edin:") illik nisbət = giriş ("İllik dərəcəni daxil edin:") numberoftimescompoundedinput = input ("Faizin ildə neçə dəfə birləşdirildiyini sayını daxil edin:") yearsinput = giriş ("İllərlə vaxt:") monthcontributioninput = input ("Aylıq töhfə məbləğini daxil edin:") # Stringlərdən daxil edilmiş girişi tam ədədlərə çevirmək prinsip = int (prinsipin çıxışı) illik nisbət = (int (illik nisbət))/100 sayıoftimescompounded = int (sayıfikrcompoundedinput) il = int (il daxilolma) aylıq qatqı = int (aylıq töhfə girişi) çap ("Daxil olan əsas:", əsas) çap ("Ondalık şəklində illik nisbət:", illik nisbət) çap ("İldə bir neçə dəfə birləşdiriləcəyi sayı:", bir neçə dəfə birləşmişdir) print ("Birləşdiriləcək illərin sayı: ", il) çap (" Aylıq töhfə: ", aylıq töhfə) # mürəkkəb faizi üstəgəl əsas ilkin sayı hesablayın = (1 + (illik nisbət/zamanlar birləşmiş)) # çap (" İlkin nömrə: ", ilkin sayı) qaldırılmış güc = (sayı bir neçə dəfə * il) # çap ("Gücə qaldırıldı:", yüksəldilmiş güc) mürəkkəbinterestplusprincipal = əsas*(ilkin sayı ** yüksəlmiş güc) print ("Mürəkkəb faiz üstəgəl əsas məbləğ:", mürəkkəb maraqlararası prinsip) # İndi gələcək depozitlərlə gələcək dəyəri hesablayın dövrün sonu # Düsturdan istifadə edərək: Aylıq Ödəniş × (((((1 + r/n)^(nt)) - 1)/(r/n)) # r = illik faiz dərəcəsi # n = Dövr başına birləşmələrin sayı (adətən aylarla) # t = pulun qoyulduğu vaxt (adətən illərlə) oneplus = (1+ (illik nisbət/zamanlar) *qaldırılmış güc2) -1)/nominalividedbynumbe roftimes) depozitlərlə gələcəyin dəyəri = aylıq töhfə*yarım çaplı çap ("Depozitlərlə gələcək dəyər:", depozitlərlə gələcək dəyər) totalamount = mürəkkəbinterestplusprincipal + futurevaluewithdeposits print ("Total Miqdarı:", ümumi məbləğ)
Tövsiyə:
Kapasitiv Giriş və LED istifadə edən Oyun Proqramı ilə Bare Arduino: 4 Addım

Kapasitiv Giriş və LED istifadə edən Oyun Proqramı ilə Bare Arduino-nu sınayın: " itələyin " Çılpaq bir Arduino lövhəsi istifadə edərək interaktiv oyun, heç bir xarici hissə və ya telə ehtiyac yoxdur (tutumlu 'toxunma' girişindən istifadə edir). Yuxarıda göstərildiyi kimi, iki fərqli lövhədə işlədiyini göstərir. Push-İki məqsədi var. Sürətlə nümayiş etdirmək üçün/v
Flysky RF Transmitteri USB + Tel Siqnal Bağlantısı ilə PC ilə işləyir + Pulsuz Simulator Proqramı: 6 addım

Flysky RF Vericisi USB + Tel Siqnal Bağlantısı ilə PC + Pulsuz Simulator Proqramı ilə Gücləndirilir: Mənim kimi olsanız, RF ötürücünüzü sınamaq və əziz RF təyyarəsini/pilotsuz təyyarənizi qəzaya uğramadan öyrənmək istərdiniz. Bu, çoxlu pula və vaxta qənaət etməklə əlavə əyləncə verəcək, bunu etmək üçün RF ötürücünüzü sizə bağlamağın ən yaxşı yolu
Python Proqramı ilə Əlaqə Sahəsi Diaqram PV: 4 Addım
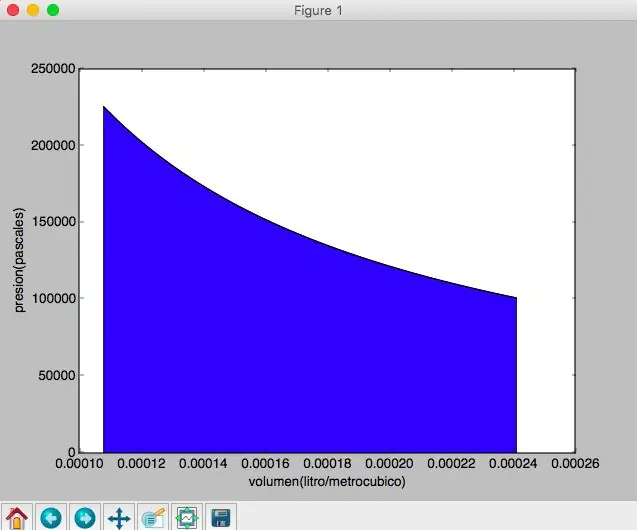
Proqramın Python Proqramı PV Şöbəsi: Proqramın bütün proqramlarının diaqramı PV -nin diaqramı ilə heç bir əlaqəsi yoxdur. Bu proqramlar ən çox qazana biləcəyiniz zaman müəyyən edilə bilər
ISU Tələbəsi olaraq Pulsuz Proqramı Necə Yükləmək olar (Microsoft, Adobe və Təhlükəsizlik Proqramı: 24 addım

ISU Tələbəsi olaraq Pulsuz Proqramı Necə Yükləmək olar (Microsoft, Adobe və Təhlükəsizlik Proqramı: Adobe üçün: 1 -ci addıma keçin. Microsoft üçün: 8 -ci addıma keçin. Təhlükəsizlik üçün: 12 -ci addıma keçin. Azure üçün: 16 -cı addıma keçin
Üç Fazlı Transformatorun Mühafizəsi üçün Faiz Diferensial Rölesi: 7 addım

Üç Fazlı Transformatorun Mühafizəsi üçün Faiz Diferensial Rölesi: Bu Təlimat kitabında, çox yayılmış bir mikrokontrolör lövhəsi olan Arduino istifadə edərək Yüzdəlik Diferensial Röleyi necə edəcəyinizi sizə göstərəcəyəm. Güc transformatoru enerji sistemində enerji ötürülməsi üçün ən vacib avadanlıqdır. Evin təmir xərcləri
